WFST加权有限状态转换机-上

2025/7/9 算法算法加权有限状态转换机 WFST

WFST(Weighted Finite-State Transducer)：加权有限状态转换机，由有限状态接收机拓展而来，在领域常被称为“解码器”。
WFST不需要更新（静态解码网络）

然后先了解一下FA有穷自动机,
DFA确定有穷自动机
NFA非确定有穷自动机

有穷自动机(FA)

自动机(Automaton)：就是一个代码块,只做一件事——接收输入值，和状态值，输出同为状态值的结果。
有限(Finite)：是指自动机接收、输入的状态种类是有限的。
确定(Deterministic )：是指自动机的输出状态是单一的一个状态。

关键组成部分：

状态（Q）：一个有限的、非空的状态集合。这些状态代表系统可能处于的内部配置。例如：{q0, q1, q2}。
输入符号（Σ）：一个有限的、非空的输入字母表（符号集合）。例如：{0, 1}。
起始状态（q₀ ∈ Q）：机器开始处理输入字符串时处于的状态。
接受状态/终结状态（F ⊆ Q）：一个状态集合。如果机器在处理完整个输入字符串后停在这个集合中的某个状态，则该字符串被接受。
转移函数（δ : Q × Σ → Q）：核心部分！这是一个函数，定义了系统如何从一个状态转换到另一个状态。
- 给定一个当前状态（q ∈ Q）和一个当前输入符号（s ∈ Σ），转移函数唯一确定地指定下一个状态（q' ∈ Q）。
- 数学表示：δ(q, s) = q'

NFA示例

think：NFA可以有丝分裂（可以保留多种可能）
注意：在非确定有限自动机（NFA）中，ε条件（epsilon transition，或称ε转移）是一种特殊的转移方式，表示自动机可以在不消耗任何输入符号的情况下从一个状态转移到另一个状态。ε（epsilon）代表空字符串（即没有输入字符）。
再注意：a*b（即任意数量的 a 后接一个 b），a*b*c 描述的语言是：任意数量的 a（包括零个），后接任意数量的 b（包括零个），最后以一个 c 结尾。

设计目标： 让机器能够识别以“01”结尾的串（比如："01", "101", "1101", "010101" 等），拒绝不以“01”结尾的串（比如："00", "10", "11", "010" 等）。

状态设想：

q0: 初始状态，也可以理解为“还没有开始认真寻找'01'结尾”或者“刚处理完可能的不合格结尾，重新开始搜索”的状态。
q1: 表示机器最近读到了一个'0'，并且希望下一个读到的字符是'1'，这个'1'如果出现，就可能是我们要找的结尾01的一部分。
q2: 接受状态，表示机器已经成功地读到了所需的结尾01。

关键转移 δ(q0, 0) = {q0, q1} 的妙处：

当机器处于起始状态 q0，并且读到一个字符 '0' 时，这个非确定性转移给了机器两种选择（或可能性，或路径）：

选择停留在 q0 (路径1):
- 想法： “我刚读到的这个0，可能不是那个作为结尾01开头的0。它可能是字符串中间的一个普通0，或者是以后可能出现的01结尾0之前的0。我需要继续按部就班地处理输入。”
- 行为： 机器保持状态 q0。
- 目的： 这种方式让机器不会错过后面可能出现的、更接近结尾的0（也就是真正的结尾01里的那个0）。
- 举例解释 (路径1为主)：
  - 输入串: "1001" (接受，以01结尾)
  - 步骤:
    - 读 '1': 只能是 δ(q0, 1) -> q0 (留在q0)
    - 读 '0': δ(q0, 0) = {q0, **q1**} -> 选择 q0 (停留)
    - 读 '0': δ(q0, 0) = {q0, q1} -> 选择 q0 (停留) (注意：这里有两个连续的0，但第一个0我们选择了q0路径，所以第二个0时我们还在q0)
    - 读 '1': δ(q0, 1) -> q0 (停留在q0) -> 结束在q0 (非接受状态) 😱 等等，出问题了！我们期望接受"1001"。这条路径失败了！但是，非确定性允许我们回溯，看看在第二个字符0读入时，选择另一条路径会怎样...
选择转移到 q1 (路径2):
- 想法： “我读到的这个0可能是我们正在等待的结尾01的起始0！我要赌一把，进入一个'期待1'的状态。”
- 行为： 机器转换到状态 q1。这个状态意味着：如果下一个字符读到的正好是1，那么我们就成功捕获到了结尾01，转移到接受状态q2。
- 目的： 这是为了立即尝试匹配以当前读到的0开头的潜在01结尾。
- 举例解释 (路径2为主)：
  - 输入串: "1001" (接受，以01结尾)
  - 步骤:
    - 读 '1': δ(q0, 1) -> q0 (留在q0)
    - 读 '0': δ(q0, 0) = {q0, **q1**} -> 选择 q1 (这条是新路径!)
    - 读 '0': δ(q1, 0) = ？ (看转移函数定义) -> 根据上面的定义 δ(q1, 0) = ? 没定义！等下看我们前面定义 δ(q1, 1) = q2，但 δ(q1, 0) 我们没定义。按NFA规则，没定义意味着 δ(q1, 0) = ∅ (空集)。读 '0' 时没有可用的转移！ -> 这条路径卡死了 😱
  - 还是不行！

改进设计：处理连续 0 的问题 - 加状态 q1 遇到 0 的转移

第二次尝试（路径2）在第三个字符0卡住了。问题在于：当处于q1（期待1的状态）却读到了0时，机器不知道怎么处理了。我们需要让机器能从q1状态读0继续存活。

状态 q1 遇到 '0' 时：
- 想法： “糟糕，我刚在q1期待一个1来结束01，但读到的是0。这意味着前面读到的那个让我进入q1的0并不是结尾01的起始0（或者说，真正的结尾01还没开始）。怎么办？没关系，刚读到的这个新的0，它有可能成为新的潜在结尾01的起始0啊！”
- 设计： δ(q1, 0) = {q1} (或者更严格地说，NFA中有时会写成δ(q1, 0) = {q1})
- 行为： 机器保持在 q1 状态。本质上是把这个新读到的0当作潜在结尾01的第一个0，并且继续期待下一个字符是1（因为现在它还在q1状态）。

改进后的NFA定义 (关键修正):

Q = {q0, q1, q2}
Σ = {0, 1}
q0 = q0
F = {q2}
δ:
- δ(q0, 0) = {q0, q1} // 读0：可留在q0或转到q1（非确定性）
- δ(q0, 1) = {q0} // 读1：只能留在q0
- δ(q1, 0) = {q1} // (新增/修正！) 读0：保持在q1(把这个新0当作新起点)
- δ(q1, 1) = {q2} // 读1：满足期待，进入接受状态q2 (关键匹配点!)
- δ(q2, 0) = ∅ // 接受状态读任何字符都无转移（可选，也可定义，但通常到接受状态后行为不重要）
- δ(q2, 1) = ∅ // 同上

示例详解: 输入 "1001" (接受)

起始: 当前活动状态集 = [q0]
读第一个字符 '1':
- 只有 q0 状态 -> δ(q0, 1) = {q0}
- 新活动状态集 = [q0]
读第二个字符 '0':
- q0 状态 -> δ(q0, 0) = {q0, q1} (非确定性分支点!)
- 新活动状态集 = [q0, q1]` (并行追踪两条路径)
读第三个字符 '0':
- 处理 q0 状态: δ(q0, 0) = {q0, q1} (又分支！但在当前路径上选择) -> 假设选择 q0 -> 路径1状态: q0
- 处理 q1 状态: δ(q1, 0) = {q1} -> 路径2状态: q1 (这里利用了新定义的转移！)
- 新活动状态集 = [q0, q1]` (两条路径仍然活跃)
读第四个字符 '1':
- 处理 q0 状态: δ(q0, 1) = {q0} -> 路径1状态: q0
- 处理 q1 状态: δ(q1, 1) = {q2} -> 路径2状态: q2 !!!!! (匹配成功!)
- 新活动状态集 = [q0, q2]`
结束检查: 当前活动状态集 [q0, q2] 包含接受状态 q2 -> 接受该字符串！

关键点解释:
当第二个字符 '0' 被读取时，机器通过非确定性创建了两条并行的“世界线”（路径）。一条（q0 -> 选择 q0）继续漫无目的地前进；另一条（q0 -> 选择 q1）则严肃地认为这可能是结尾 01 的开始。
当第三个字符 '0' 到来：
在“漫无目的”的那条线上（状态 q0），机器可以继续停留或者开启新的 q1 分支，但这条线在本例中继续选择停留 q0。
在“严肃对待”的那条线上（状态 q1），机器期待的是一个 1，但读到了 0。我们修正后的转移 δ(q1, 0) = {q1} 救活了这条路！它把这个新 0 解释为一个新的潜在 01 起始符（就像最开始进入 q1 时看待那个 0 一样），所以机器保持 q1 状态，期待下一个是 1。
当第四个字符 '1' 到来：
在“漫无目的”的那条线（q0），读 1 只能留在 q0。
在“严肃对待”的那条线（q1），读 1 完美匹配了它期待的模式！ δ(q1, 1) = q2。这条路成功地转移到了接受状态 q2。
因为最终状态集中包含 q2（这条路径成功），所以整体接受 "1001"。另一条路径最终在 q0 失败了，但NFA只看是否有至少一条路径成功！

下图来源于知乎
展示了由NFA到DFA的确定化

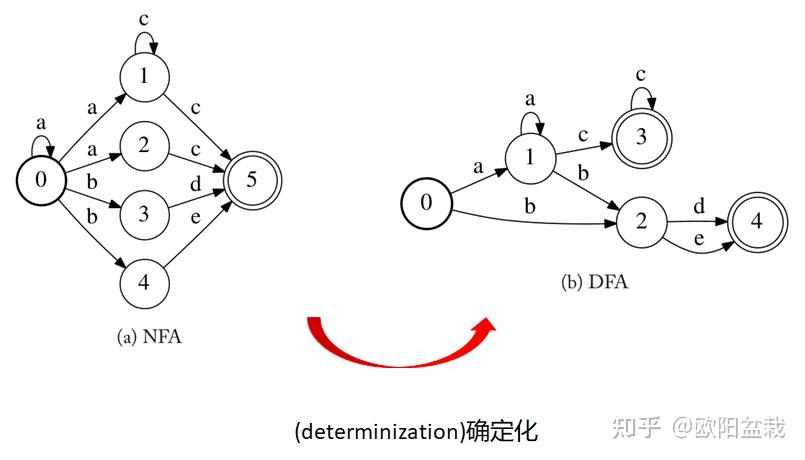
一、为什么要确定化（Why）？

去除不确定性： NFA 在同一个状态下，对于同一个输入符号，可能有多个转移选项，甚至可以通过 ε（空串）进行转移而不消耗任何输入字符。这种不确定性给 NFA 的执行（模拟运行）带来了复杂性，通常需要回溯或并行探索所有可能的路径。
简化实现和执行： DFA 是确定性的，即：
- 没有 ε 转移。
- 每个状态对于每个可能的输入符号，有且只有一个确定的后继状态。
  这使得 DFA 的执行非常简单高效：从一个状态读取一个输入符号，必然转移到一个唯一确定的下一个状态。
统一模型与算法： 许多与正则语言相关的理论（如最小化）和算法（如词法分析）是建立在 DFA 模型之上的。将 NFA 转换为等效的 DFA 使我们能够利用这些更成熟、更高效的理论和工具。
基础性证明： 该转换过程本身证明了 NFA 和 DFA 在识别语言的能力上是等价的（即它们都识别精确的正则语言集）。这是计算理论中的一个重要结论。

二、确定化流程（流程是什么？） - 子集构造法（Subset Construction）

👍下面的好像默认自己的状态可以由空跳转。（也可能是NFA的特性）-
~~我没看见自环~~

核心思想是将 NFA 中的一组可能状态（一个“集合”）打包成 DFA 的一个单个状态。DFA 的状态对应于 NFA 状态的子集。
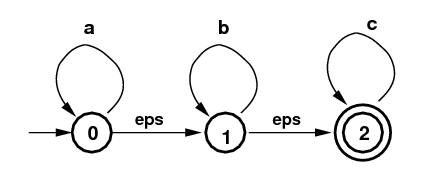
子集构造的核心概念是ϵ-闭包(ϵ−closure)算法。比如下图所示的NFA，它可以识别的语言是”a*b*c*“(请读者验证)。ϵ-闭包算法的输入是一个NFA的状态集合，比如{1}，它的输出也是一个状态集合，其中输出集合的每一个状态都是可以从输入状态经过全是ϵ的边跳转到这个状态。因此如果输入是{1}，那么它的ϵ-闭包是集合{1,2}，因为1可以通过空跳转到自己，而1也可以通ϵ跳转到2。类似的输入{0}的ϵ-闭包是集合{0,1,2}，因为0可以通过ϵ跳转到1，而1又可能通过ϵ跳转到2。

图：识别”a*b*c*“的NFA

图：识别”a*b*c*“的DFA

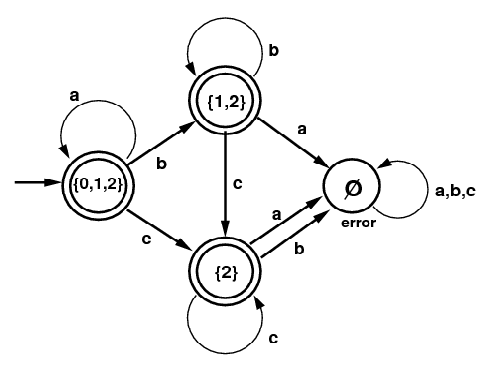
子集构造的过程如下图所示。NFA的初始状态是0，我们首先得到它的ϵ-闭包{0,1,2}，我们把它作为DFA的一个状态，因为它包含NFA的初始状态0，因此它也是DFA的初始状态；同时它包含NFA的终止状态2，因此它也是DFA的终止状态。

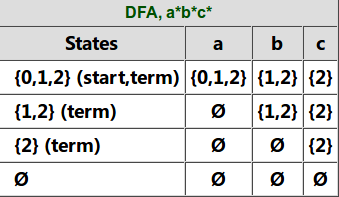
接着我们看DFA的状态{0,1,2}输入字母a的情况，状态0输入a还是0，而状态1和2不能输入a，因此{0,1,2}输入a可以得到0，而0的ϵ-闭包是{0,1,2}，因此{0,1,2} -a->{0,1,2}。再看{0,1,2}输入b的情况，0和2不能输入b，只有状态1遇到b后还是状态1，因此{0,1,2}遇到b的”直接”输出是{1}，而{1}的ϵ-闭包是{1,2}，因此最终{0,1,2}-b->{1,2}。类似的，我们可以得到{0,1,2}-c->{2}。

这个时候的状态除了{0,1,2}又多了{1,2}和{2}，我们再来看第二行状态{1,2}的跳转。首先是{1,2}输入a，跳不到任何状态，因此输出是空集∅∅，空集的ϵ-闭包还是空集。然后是{1,2}输入b，2遇到b没有，1遇到b还是1，然后1的ϵ-闭包是{1,2}，因此{1,2}-b->{1,2}。后面的过程都是类似的，当处理完空集后没有产生任何新的状态，因此整个过程结束。

图：通过子集构造把NFA转换成DFA

学习资料来源：

LOADING

WFST加权有限状态转换机-上

有穷自动机(FA)

NFA示例

一、为什么要确定化（Why）？

二、确定化流程（流程是什么？） - 子集构造法（Subset Construction）